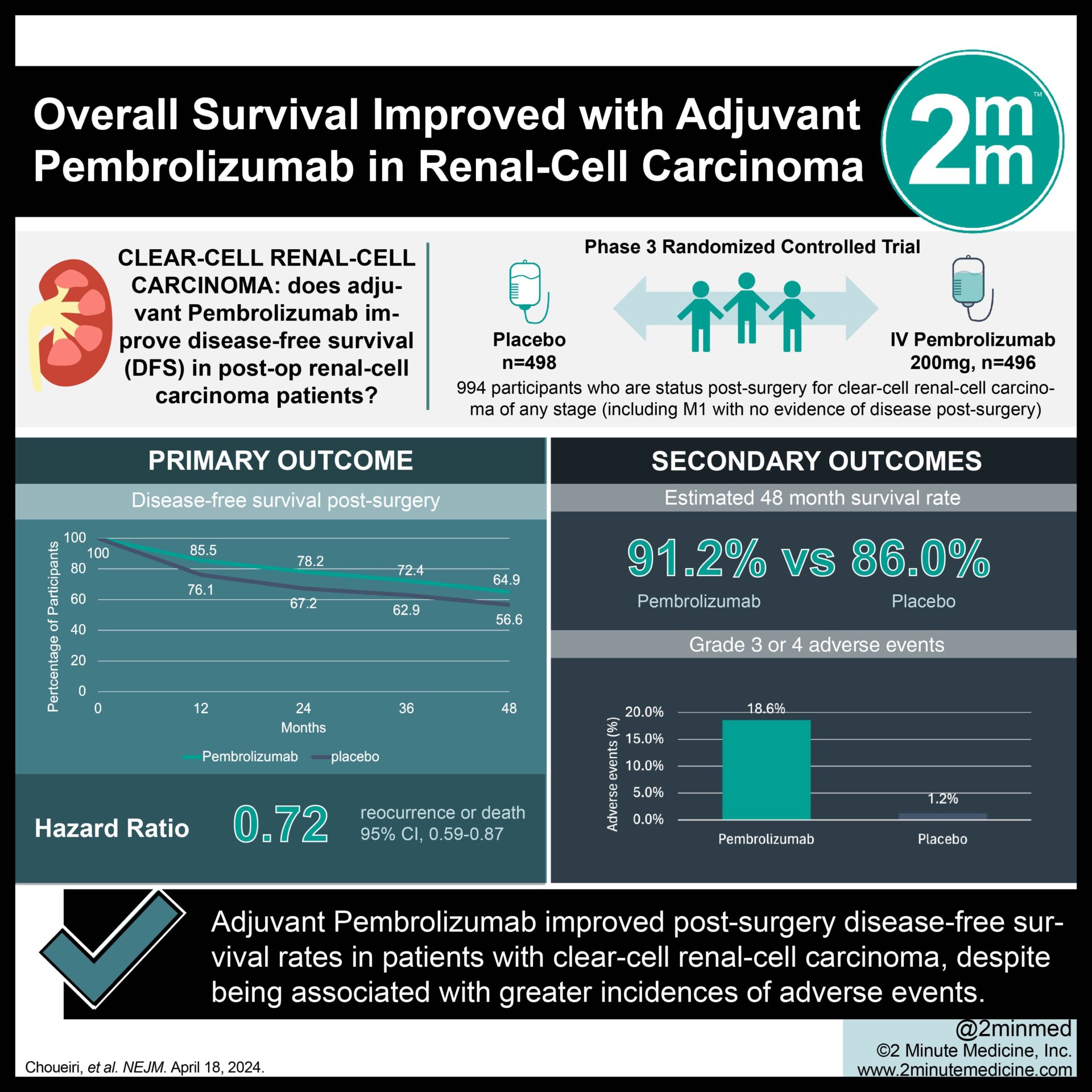
Semiparametric transformation models for failure time data consist of a parametric regression component and an unspecified cumulative baseline hazard. The nonparametric maximum likelihood estimator (NPMLE) of the cumulative baseline hazard can be summarized in terms of weights introduced into a Breslow-type estimator (Weighted Breslow). At any given time point, the weights invoke an integral over the future of the cumulative baseline hazard, which presents theoretical and computational challenges. A simpler non-MLE Breslow-type estimator (Breslow) was derived earlier from a martingale estimating equation (MEE) setting observed and expected counts of failures equal, conditional on the past history. Despite much successful theoretical and computational development, the simpler Breslow estimator continues to be commonly used as a compromise between simplicity and perceived loss of full efficiency. In this paper we derive the relative efficiency of the Breslow estimator and consider the properties of the two estimators using simulations and real data on prostate cancer survival.© 2023. The Author(s), under exclusive licence to Springer Science+Business Media, LLC, part of Springer Nature.